今回は5回目です。
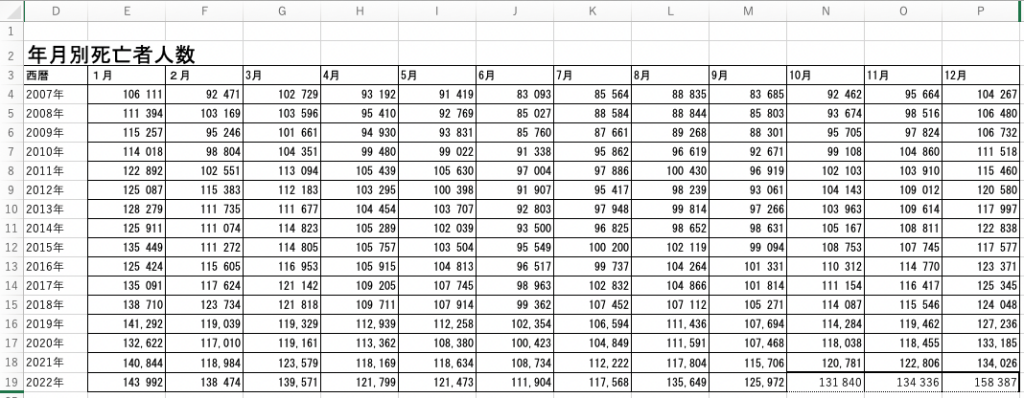
前回の終わり際に作成したエクセルの表を再度見てみましょう。
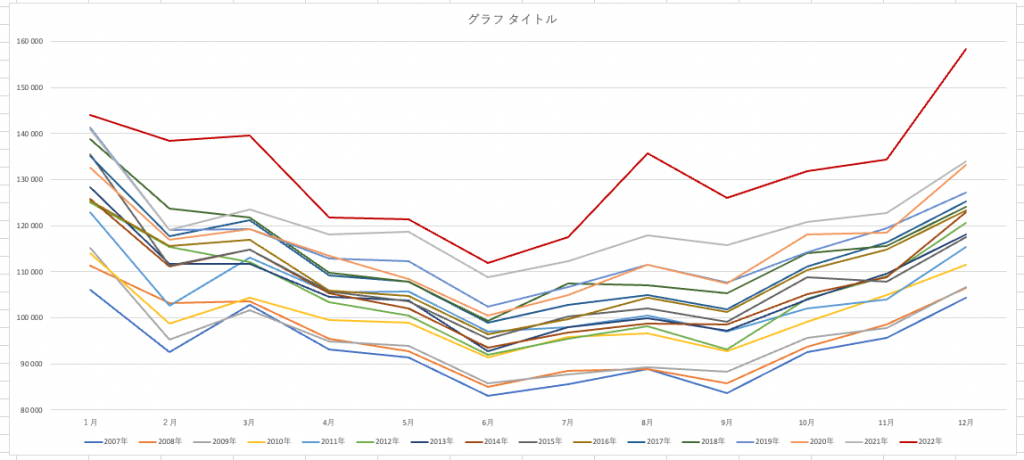
そしてここから作成した年別のグラフが下記でした。
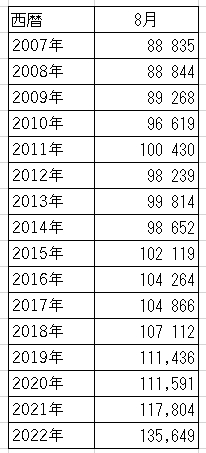
2022年は全体的に他の年よりも高いように見えますが、今回の目的としている8月だけを抜き出します。
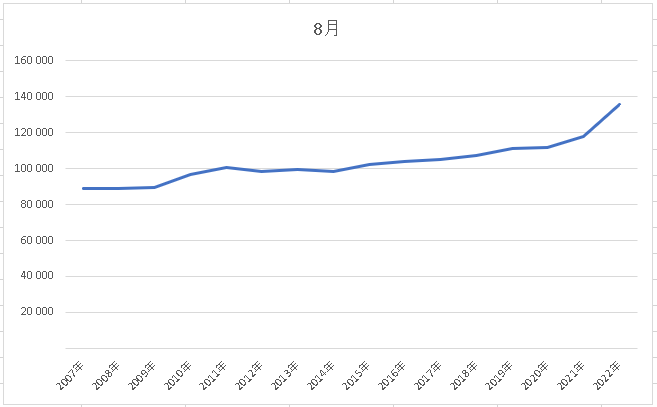
さて、この表全て(「西暦」セルから「135,649」セル(2022年の死亡者数)まで)を選択して、作成した折れ線グラフがこれになります。
2007年から2021年までを見ると、なだらかに上昇しているようです。但し、東日本大震災のあった2011年は2010年に比較して上昇が大きいですね。2022年は、2011年と比べても相当上昇が大きい事が分かります。
さて、ここから基本的な数理統計分析手法を行ってみます。
単回帰分析です。AIが流行り出してからは皆さんも聞いたことがある分析名だと思います。
単回帰分析とは、2つの異なる情報群を数式で表現し、その2つの情報群に関係性があるかを検証する分析手法です。
それでは順を追って進めて行きます。
(1)散布図を作る
今回の「2つの情報群」とは、1つは各年の8月の死亡者数です。そしてもうひとつは「西暦」です。西暦?? これって数式になるの?って疑問ですよね。「2022年」ではなく「2022」なる整数として考えます。そして、先ほどの各年の8月の表の西暦部分を整数に置きかえます。
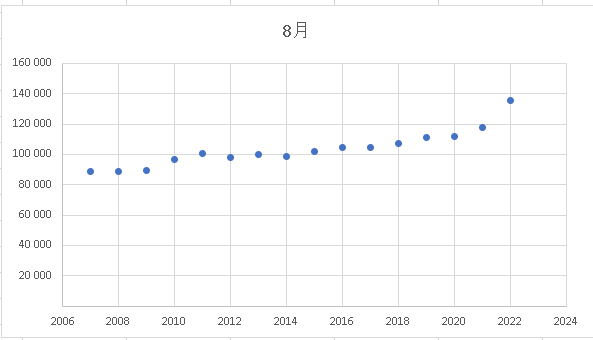
そして、表全体を選択し今度は散布図を作ります(「挿入」→グラフグループの「散布図」)。下記のような図が表示されると思います。
そうです、先の折れ線グラフが点になっただけです。しかし、これは折れ線グラフとは目的が違うます。横軸(2006~)の数字と縦軸(20000~)の数字の接点が点と見てください。 そして各点のばらつき状態を観察してほしいのです。 やや上下していますが、横の数字が増えるほど縦の数字が増えた場所に点が存在しているばらつきに見えます。 うっすらと「斜めの直線」が見えてきますね。但し横の数字「2022」は飛んじゃってますが・・・・。
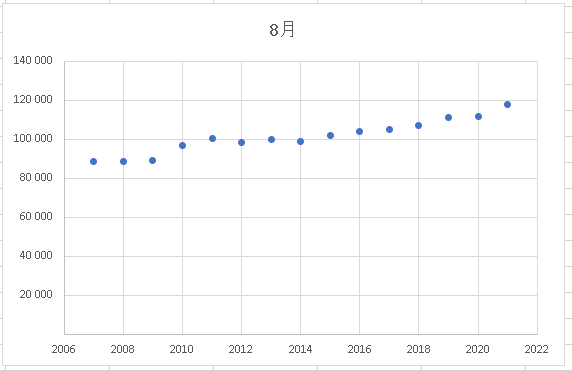
ここで、2022と135649のペアの点を外して再度散布図を作ってみると、かなり斜めの直線が透けて見えてきます。
単回帰分析を行う場合、この散布図で大まかなグラフの「形」をイメージする事が大事です。そして、併せて大事なことは、ここで扱ってる情報群が、年を進めるごとにどのような傾向となるかを、社会的や常識的に把握することです。
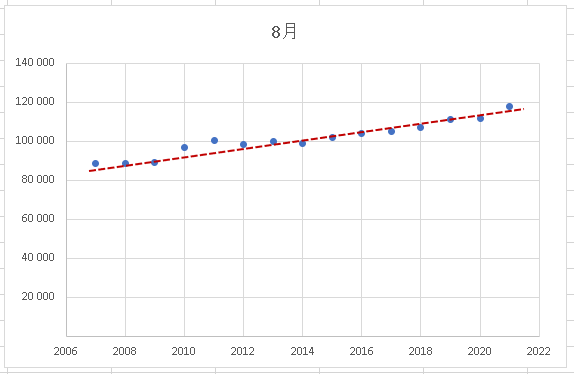
今回は日本の死亡者数です。ここ数十年間の日本は、少子高齢化の社会で、高齢者が増加しています。 人間は高齢になるほど死亡率は高まります。平均寿命も伸びていますが高齢者が増加すれば、死亡者数も増加する事になります。今回は、単回帰分析でも最も基本的な一次回帰(直線グラフの回帰)を行ってみます。2つの情報群をXとYとした時に、Y=a×X+b (ここでa、bは固定の数字)で数式化したものが一次式のグラフです。
下記のような直線がイメージできますね。
今回はここまでとします。
次回は、このイメージした一次回帰の数式を算出する方法と、その数式が2つの情報群の関係性の強さからみて意味があるのか?を判断する方法となります。