今回は7回目です。前回で単回帰(一次回帰)分析を行い、結果が下記となりました。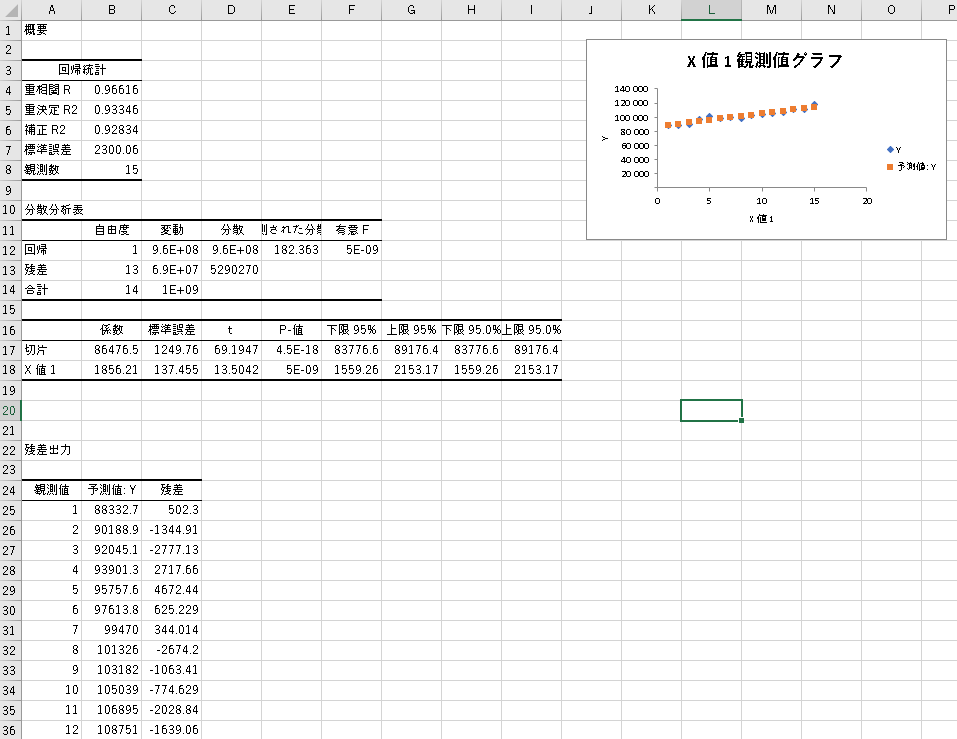
まずこのシートで見るべき項目と数値は「相関」です。
ここ3年ほど、世界的な感染症をテレビ番組などで取り上げた際に、様々なグラフや表が表れて、「この数字と感染数は相関関係があるのでは?」など、一般的に使われ出しました。
字のごとく「あるものと、違うあうものの間に関係があるか?」を数値化しています。
-1から1までの数値を取るのですが、先のテレビなどでは「相関係数が0.5もあるので・・・」等、首をかしげたくなる表現が平気で出るので不安になっています。
詳細は省きますが、数理統計学を学校で学んだ人からすれば、基本的に相関係数は0.9以上(-0.9以下)でなければ、ぐっと関心を持ちません。
今回の場合、「重相関係数=0.96616」となっており(重相関と表示されているが今回は単相関だがエクセルでは単も重に入っている表現らしいです)、相当ぐっと関心が来ます。
「正の関係性がかなり高いようだ」と考えます。
さて今回の回帰分析で算出した関係式はどこなあるかというと、「切片」と「X値1」の「係数」で分かります。 Yを死亡者数、Xを年(2007年が1、以降1年づつ年が進む)としたので
Y=86476.5+1856.21×X となります。 86476.5は切片の係数、1856.21はX値1の係数です。
シートの下のほうに「観測値」「予測値:Y」があります。この式でXに1を入れるとYは88332.7とこの表の予測値にピッタリなりますね。
以上、これでおしまい!ではありません。ここからが大事なのです。
確かに相関係数は、0.96616と高いのですが、この式は意味のある式なのかくを確認する必要があります。その為に確認すべき項目が「有意F」です。 分散分析表の一番右端にあります。
今回有意Fは「5E-09」です。この「E-●●」の見方は、「10のマイナス●●乗」を表します。小数点以下が非常に長い(非常に小さい)数値なのでこのように表現しています。ちなみに5E-09とは、0.000000005と非常に小さい数値です。詳細は省きますが、有意F値は、X値1のP値と等しくなります。
この有意Fが0.05未満であれば、XとYの関係を表しているこの式は「でたらめに作成した式」とは言えないとなります。回りくどいのですが数理統計ではこのような表現をよく使います。
簡単いえば「XとYの関係をまずうまく表しているようだ」でしょうか。
ここまでで、今回回帰分析で算出した式が 、2007年から13年間の毎年8月の死亡者数との関係を表しているに使えそうだと分かりました。
ちなみにこの式の「1856.21」とは、「毎年毎年8月に死亡者数は 1856人増えている」て事になります。この増加覚えておきましょう。
次回は、この式に対して2022年8月の死亡者数をグラフに表示して、目で見たグラフとの関係と、その値が数理統計でどのように判断できるのか?を説明していきます。
